3d dimension of the photograph, Part 1
It’s been almost a century and a half since the first stereoscopic photographs were presented at the Universal Exhibition of London in 1851. For many years after that stereo photography has rapidly developed and new devices for shooting and demonstration have been created. Attractions, where visitors were shown stereoscopic pictures of far-away countries and historical events, were very popular in the Old and New World. In the course of time the interest in stereo photography languished as there appeared new ways to amuse oneself such as cinematography. However, with the development of new technologies we are witnessing the increasing interest in this ancient kind of visual art. Computers as well as new ways of viewing significantly simplify the process of creating a stereo image. This makes stereo photography popular all over again. This article begins the series of publications where we will observe the mechanism of stereo image creating and some methods of producing.
Terms
Accommodation – crystalline lens convexity change allowing the image of the objects located at different distances to be focused on the retina.
Complementary colors – two colors that produce white color when combined, e.g. blue – yellow, cyan – red, blue-violet, yellow-green.
Convergence – sight line converging while looking at the objects located at a small distance.
Stereo base – the distance between the positions for taking the left and right photos.
Stereo pair – two photos of the same scene (object) taken by two identical cameras from two different points distanced horizontally from each other (at the stereo base distance).
Parallax – the shift of the object you are looking at caused by viewing angle change.
Zero parallax object (zero parallax point) – the object in the scene that does not have parallax (it is not doubled on the final image), it will seem as if located in the key plane of the stereo photography. The rest of the scene objects will seem either in front of it as if hanging in the air (foreground objects) or behind it as if put in the background (background objects).
Physical basis of stereoscopic vision
The human eye can sense light. The light is one of the electromagnetic energy forms characterized by wavelength. Waves with the wavelength of about 300-800 nm range allow us to sense color and brightness. Objects can reflect or sometimes radiate light. That is why they are visible for the human eye.
A number of phenomena allow people to get the idea of the three-dimensional world around us: geometric and atmospheric perspectives, shadows and flecks on the objects and their relative sizes. For a long time painters have been using techniques simulating these phenomena to show the depth of three-dimensional objects drawn on the flat.
The other reason why we can estimate the location of objects in space is the way they move relative to each other when we change our viewing point (closer objects move against more distant ones). It helps us to evaluate how far objects are located from us while we are watching a movie or looking at the scenery out of the train window. Our accumulated experience of perceiving the world allows us to interpret the above phenomena as the evidence of three-dimensional space while observing real objects, viewing pictures and photos or watching movies. The effect does not depend on whether we are looking with both eyes or only with one eye.
While looking at an object in real life, we use one more mechanism of human vision called accommodation. The human brain evaluates the effort needed to focus the eye and it allows us to get additional information about the location of objects in space.
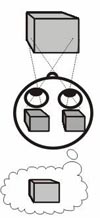
Nature also gave people a more precise instrument – binocular vision – a pair of eyes located symmetrically at the distance of 60-70 mm. Due to this a person sees the world from two points at the same time. As a result, images perceived by the left and right eyes slightly differ. These two images are called a stereo pair. Analyzing differences between the images of this stereo pair, the human brain receives information about the depth of objects being watched and the distance to them.
The perspective (seeming) shift of the object being viewed caused by the changed viewing point is called parallax and is the main reason we perceive three dimensions of the world (Fig. 1).
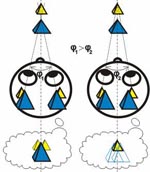
The mechanism of stereoscopic vision called convergence or divergence (depending on the direction of the action) plays an important role in evaluating distances.
Convergence means converging sight lines while looking at objects located at a small distance. Divergence (moving sight lines apart) occurs while looking into the distance. This makes objects located at the intersection of the sight lines look clear and objects located farther or nearer look doubled. You can easily see this doubling if you carefully look at the object located at arm’s length from your eyes (for example, your finger) and pay attention to the farther objects. Usually, we do not even notice this doubling, but the brain processes it and it helps to judge about how distant objects are. Besides, the brain takes into account the angle of sight line convergence (Fig. 2).
It is this mechanism of human vision that is used in most methods of viewing stereoscopic (three-dimensional) images.
When your attention is focused on closer objects (blue pyramid), more distant objects look doubled. When you attention is focused on more distant objects (yellow pyramid), closer objects look doubled
Stereo photo shooting methods
All methods described below are based on the principle of separate observation – the left eye sees the left image of the stereo pair, while the right eye sees the right image. These methods differ in how the separation of images in the stereo pair is achieved. Thus, to create a stereo photo, you need a stereo pair. Usually, you get it by taking photos of the same object from two points that simulate the position of the human eyes. The distance between the positions for taking the left and right photos is called stereo base.
The size of the stereo base plays the key role in creating a stereo photograph. If you make stereo photos of scenes that are up to 3-5 meters away, it is quite enough to use the base of 65-70 mm, i.e. approximately the distance between the human eyes. When the distance to the objects being shot increases, the stereo base should be also increased in order to get a good stereo effect. You can use the following formula to calculate the approximate stereo base:
B=0.03*D,
B is the stereo base and D is the distance to the closest object in the scene being shot.
The coefficient of 0.03 is used due to the angle of sight lines convergence (approximately 1-2°) that provides optimal conditions for watching a stereo effect.
There are also more complicated models for calculating the stereo base taking into account the relative position of objects in the scene, camera parameters and the way the final stereo photo will be viewed.
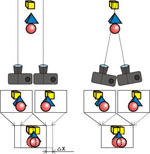
It is possible to use two methods to take a stereo photo: parallel and intersectional. When the parallel method is used, the direction of the optic axis of the camera lens does not change (Fig. 3, a), but when the intersectional method is used, the optic axis of the lens is turned so that it is always directed at the central object of the scene (Fig. 3, b). The intersectional method models the convergence of the human eyes.
The advantage of the parallel method is its simplicity – you do not have to turn the camera, the disadvantage of this method is that you have to additionally process the photos (compensational shift). A compensational shift means moving photos relatively to each other so that to get zero parallax (no doubling) for one of the objects in the composition (zero parallax object). This process models the convergence of the eyes after the stereo pair has been taken. When you view the stereo image, zero parallax objects will be perceived as located on the key plane; objects located closer to the photographer in real life will have negative parallax and seem as if situated in front of the zero parallax object; objects located in real life farther than the zero parallax object will have positive parallax and will be perceived as if they are in the background of the image. In Fig. 3 you can see a compensational shift (∆Х is the size of the compensational shift) where the stereo pair is superimposed by the blue pyramid – this object has zero parallax.
After you make this shift, the horizontal size of the images gets smaller – the stereo pair includes only those parts of the images that are superimposed on the initial images. Actually, it is possible not to make the compensational shift. In this case, all objects of the scene will have negative parallax and seem as if they are in front of the plane the image is printed on. In this case, only “infinitely distant” objects will have zero parallax.
With the intersectional method it is all vice versa, the process of taking photos becomes more complicated (you have to turn the camera), but the images you get are already a stereo pair and if you took them without inaccuracies, you may need no additional processing.
The intersectional method sometimes allows you to get a stereo image that reproduces the natural perception more accurately. But the difficulty of this method is that the parallax of distant objects may turn out to be too large. It may reduce the comfort while viewing the stereo image. One more disadvantage of the intersectional method may result in different-angle affine distortions which may introduce some dissonance in the image being viewed. That is why this method is used to take photos under specially created conditions.
Due to its simplicity and the stability of its results, the parallel method is used more often. And computer processing makes creating a compensational shift an easy task.
Equipment for taking stereo photos
There are special two-lens cameras for taking stereo pairs (Fig. 4, a) and lens stereo adapters for regular cameras (Fig. 4, b). The advantage of these devices is that they allow you to get a ready stereo pair at once and can be used to take photos of moving objects.
You can take stereo photos with a regular camera as well. And this method even has its advantage – you can easily choose the size of the stereo base. To make the process more comfortable, a special rail (tripod adapter) is used to allow you to move your camera horizontally (Fig. 5).
Serial-frame shooting is used in lenticular stereography. The process of shooting is as follows: the camera is based on the tripod adapter at the last position and a shot is taken. For the next shot the new position is selected. To get a high-quality stereo image you will nned from 10 to 18 shots.
However, an advantage as usual comes together with a disadvantage: the necessity to move the camera during the shooting process makes it more difficult to take photos of moving objects – the scene will change while you will be moving your camera and, as a result, you will not get a stereo pair.
The quickness of shooting and the flexibility of choosing a stereo base can be achieved with a system consisting of two or more cameras fixed on one rail and having synchronized shutters. The disadvantage of such a system is the difficulty of setup: camera lens must have the same characteristics. They must be precisely aimed and adjusted. Besides, the cost of this system increases.

Fig. 6 System for stereo photography consisting of two cameras (picture from www.crystalcanyons.net)
To get stereo photos with a look-around effect, multi-frame shooting is used. In this case, you take photos not only from the extreme points of the stereo base, but also between them – usually, it is from 6 to 12 shots. As a result, you get a whole set of stereo pairs allowing the viewer as if to look behind objects in the foreground. It is possible to take such photos with a regular single-lens camera using a tripod adapter (Fig. 5).
There are also special cameras capable of taking a set of stereo pairs at once, which allows you to take photos of moving objects (Fig. 7)